What even is differential privacy?

SVG Icon Editor

Author: Moritz Knolle

Machine learning (ML) technologies are set to revolutionize various fields and sectors. ML models can learn from text, image and various other forms of data by automatically detecting patterns. Their successful application, however, relies heavily on access to extremely large datasets (some state-of-the-art language models are trained on the whole internet). For many interesting applications, such datasets contain sensitive information (e.g. medicine and patient data), thus precluding the application of ML. This is because ML models store some of their training data nearly verbatim and have been shown to be susceptible to a wide range of attacks [1, 2, 3], which can reveal sensitive aspects of the training data.

In this blog post, we will provide a short and simple explanation of differential privacy (DP), a technical solution that preserves privacy while allowing us to still train accurate ML models on datasets containing sensitive information. DP provides provable and quantifiable privacy protection to individuals sharing their data for model training or, in fact, any other form of data processing.

A non-technical primer on DP

In essence, DP states that the result of any data processing is "roughly" the same, no matter which individual's data is removed from (or added to) a dataset. Conversely, this means that a differentially private computation cannot depend very much on any single individual's data in a dataset. As a result, DP prevents potential adversaries from learning specific details about any individual in a dataset while still allowing anyone to study trends and population characteristics of the data. Putting this into context: DP applied to a pancreatic cancer dataset prevents anyone from inferring if a given patient was a member of this dataset (and thus if they have cancer), while still allowing researchers to study the properties of pancreatic cancer and its causes.

DP is inherently tied to the concept of public release of summary statistics, where "summary statistics" can also be a machine learning model (or e.g. the average height ). In fact, the output of any computation that involves private information in some form is considered sensitive and is thus releasable under DP. The terminology used to describe DP often revolves around "queries on databases/datasets" because this phrasing captures the essence of a wide array of operations, from statistical analysis to machine learning, maintaining generality across applications. Finally, achieving DP involves the strategic insertion of randomness somewhere into a computation, which serves to obscure the contributions of individual data points.

Towards a slightly more technical definition

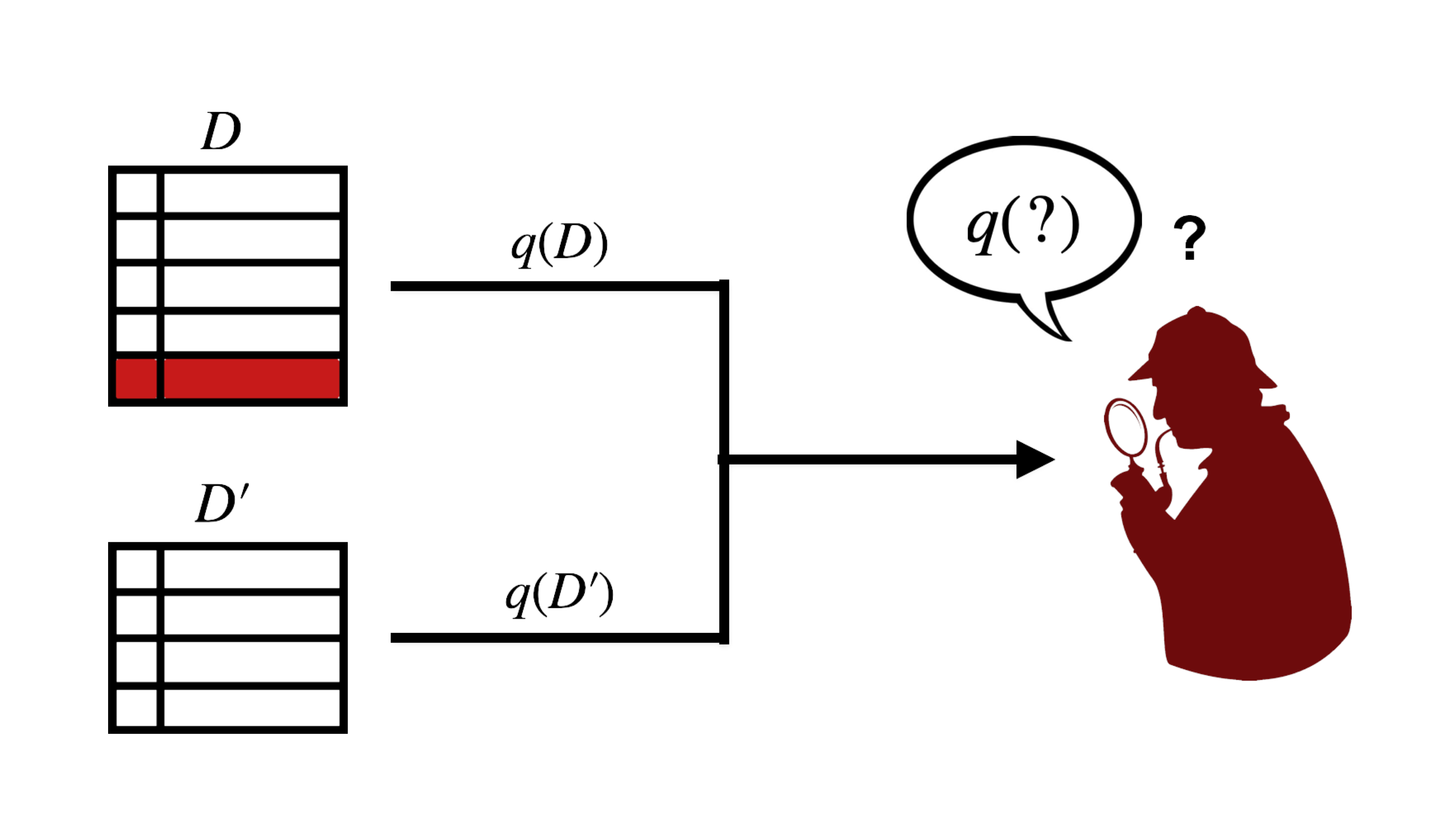
DP relies heavily on the concept of dataset adjacency, which might sound complicated at first but really isn't. Two datasets D and D^\prime are called adjacent (denoted by D \simeq D^\prime) if they differ by one individual's data (typically one row in a dataset; shown below in red):

Being able to establish this adjacency relationship is essential for satisfying DP. DP is so powerful because it protects against worst-case privacy leakage, no matter how much an individual's data stands out from the rest of the dataset. This means that D and D^\prime are picked such that the difference between the output of the query q (which we wish to privatise) under D and D^\prime is maximised (i.e. \sup_{D\simeq D^\prime}{\lVert q(D)- q(D^\prime)\rVert_p}). This quantity is called the query sensitivity. Note that, here, we do not consider the actual values in D or D^\prime but are concerned with the maximum possible change in q(\cdot) caused by the removal of one single individual's data. For example, if q is a function that returns the number of persons that are HIV positive in a dataset, then the query sensitivity is 1. This is because the result of a counting operation can only change by a maximum value of +1 or -1 when any datapoint is removed.

Constructing a query function q that satisfies DP then simply means that any output of q is similarly likely to have been produced by D or D^\prime. A popular definition, \varepsilon-DP, requires any output of q to have multiplicatively similar probability under D and D^\prime:

    \[p\left(q(D)\right) \leq \varepsilon \; p\left(q(D')\right)\]

If q(\cdot) by itself does not achieve the above condition (this is often the case), we can add statistical noise to achieve the above condition (simple Gaussian or Laplacian noise suffices if scaled appropriately). Conversely, the above equation means that it is impossible (or very hard, depending on the choice of \varepsilon) for an adversary, attempting to break privacy, to confidently distinguish between the outputs of q(D) and q(D'). This is crucial, as not being able to distinguish between q(D) and q(D') implies a direct upper bound on how well any adversary can reconstruct any datapoint [4].

DP_adversary

For many applications achieving a small \varepsilon (sometimes called a privacy budget), that is making q(D) and q(D') basically impossible to distinguish, is difficult and usually leads to very noisy, low-quality results. Improving this, so-called, privacy-utility tradeoff is a central research focus in the DP community. ML practitioners are in luck: it was recently shown that it's possible to train highly accurate models with small privacy budgets using a few simple tricks [5].

The essence

DP provably protects privacy by preventing a query's output from changing significantly due to the removal of any individual's data in a dataset. This implies that it is impossible for anyone to learn specifics about any individual's data in dataset while still allowing legitimate users to learn trends in the dataset.

Real-world use cases

Differential privacy is in the process of becoming a mature technology and is already being deployed in a number of real-world applications involving sensitive data. Some of these are listed below:

To conclude, balancing the requirements of DP and accuracy in such large-scale applications will remain a hot topic for future research.

RELATED

  • / Molly Kennedy

    Exploring XAI Methods for Interpretability of Large Language Models

    Large Language Models can summarise text, answer questions, and classify sentiment with impressive accuracy, but their reasoning often feels like a black box. Why did the model land on that prediction? This post walks through four complementary approaches from Explainable AI (XAI) that help open up the box. Together, these methods make LLMs less opaque and more trustworthy. Full post
  • / Tzu-Yuan Huang

    Robotic Decision Making via Diffusion Models

    Robots are increasingly expected to operate in complex, real-world environments, but the machine learning methods that drive their decision-making, like reinforcement and imitation learning, often struggle with training stability and capturing the multimodal nature of behavior. This post introduces diffusion models as a powerful alternative for robotic decision making, explaining their core denoising mechanism and surveying their applications in several contexts. Full post
  • / Lukas Gosch

    A Beginner’s Guide to Certifiable Robustness

    Machine learning models, such as ChatGPT and those used in autonomous driving, are becoming essential tools in our daily lives. However, the existence of "adversarial examples" demonstrates that these systems are not free from vulnerabilities. The post, introduces the concept of adversarial examples and discusses Certifiable Robustness, a methodology designed to combat them. Full post
  • / Balian He

    Responsible Textual Generative Models (Part I): Generating Truthful Content

    This post introduces hallucination in large language models—why fluent outputs can still be wrong, what distinguishes intrinsic from extrinsic errors, and how training data, model design, inference, and alignment contribute. It surveys detection and mitigation approaches and sets up later posts on toxicity, bias, and inclusivity in responsible textual generative AI. Full post
  • / Aswathi

    Random Convolutions: A Simple Way to Boost Generalization

    Random Convolutions (RC) are a simple and effective data augmentation technique designed to improve the robustness of deep learning models, particularly in medical imaging. Instead of relying on fixed or learned filters, RC applies a small stack of randomly generated convolutional filters to input images during training. This introduces strong but controlled variations in image texture while preserving the underlying anatomical structure. By exposing models to a wide range of plausible appearance changes, Random Convolutions reduce overfitting to dataset-specific characteristics such as scanner type or acquisition protocol. In practice, RC acts as an implicit form of domain randomization, encouraging models to focus on stable, shape-based and contextual features rather than fragile texture cues. Despite its simplicity and low computational cost, RC has been shown to substantially improve generalization across institutions and imaging conditions in challenging tasks such as multiple sclerosis lesion segmentation. Full post
  • / Ahmed Abdelrahman

    Neuromorphic Computing: A Brain-inspired Approach to Robot Intelligence

    This post offers a high-level walkthrough of neuromorphic computing, why it matters for energy-efficient robot intelligence, and how SNNs, event cameras, and neuromorphic chips fit together Full post
  • / Shengqiang Zhang

    Introduction to Embodied Instruction Following

    This work explores how AI systems bridge the gap between understanding human instructions and performing real actions by learning through direct interaction with their environment. Full post
  • / Maximilian Fleissner

    From Unlucky Strikers to Statistical Learning Theory

    Using the analogy of football striker, this post explains how statistical learning theory helps us understand when we can trust model predictions and empirical averages, highlighting the challenges of generalization in modern machine learning, especially with complex models like deep neural networks. Full post
  • / Unai Fischer Abaigar

    Performative Prediction

    Machine learning systems are increasingly used to support decision-making processes. Yet, these systems do not merely reflect the world—they also reshape it. Once deployed, predictions can influence behaviors, alter policies, and redirect resources, creating feedback loops that change the very data-generating processes they aim to model. Full post
  • / Valentyn Melnychuk

    Quantifying Uncertainty of the Treatment Effects

    The post highlights the importance of moving beyond average treatment effects by quantifying the uncertainty of these estimates. It introduces a method using Makarov bounds and a Neyman-orthogonal AU-learner to provide reliable bounds on treatment effects, offering a clearer view of potential benefits and harms in high-stakes scenarios. Full post
  • / Yusuf Sale

    Conformal Prediction

    Uncertainty quantification (UQ) is paramount in deploying machine learning models for safety-critical tasks. Among other shortcomings, many UQ methods rely on strict, hard-to-test, distributional assumptions. Conformal prediction provides a distribution-free alternative and has become a standard tool in the UQ shed. Full post
  • / Sameer Ambekar

    Mitigating Domain shifts

    Adapting a deep neural network to unseen data and tasks is imperative these days, however access to target data is often available. Common target adaptation techniques including domain adaptation and generalization train for meaningful representations during source training. Recent paradigms such as Test-time training/adaptation focus on optimizing the source model on unseen data. To do so, they finetune the model on the streaming unsupervised data which is useful for practical scenarios. Moreover, these techniques can be applied to variety of tasks such as regression, classification and segmentation. Full post
  • / Lisa Wimmer

    A gentle introduction to uncertainty quantification

    Uncertainty Quantification (UQ) is considered indispensable for predictive models in safety-critical applications. Modern models, though high-performing, struggle with providing meaningful uncertainty estimates due to a number of reasons. Full post
  • / Blog Editorial Team

    Welcome to the relAI Blog

    Welcome to the relAI blog of the Konrad Zuse School of Excellence in Reliable AI (relAI). This blog will serve as a platform to share cutting-edge research and developments from our school, highlighting the significant strides we are making towards making AI systems safer, more trustworthy, and privacy-preserving. Full post
LOAD MORE